

STEPS FOR 3 EQUATION SYSTEMS PLUS
Upon checking we can see that -4 times -5 plus 1 is in fact 21. This allows us to get the solution, x = -5. First we must cancel the addition by 1 by subtracting 1 from both sides. Substituting it into the original equation yields.

Using our example above, we can see that our solution, x = -7 is correct because it checks. Once simplified, both sides of the remaining equation should be equal to each other if the original answer is correct.
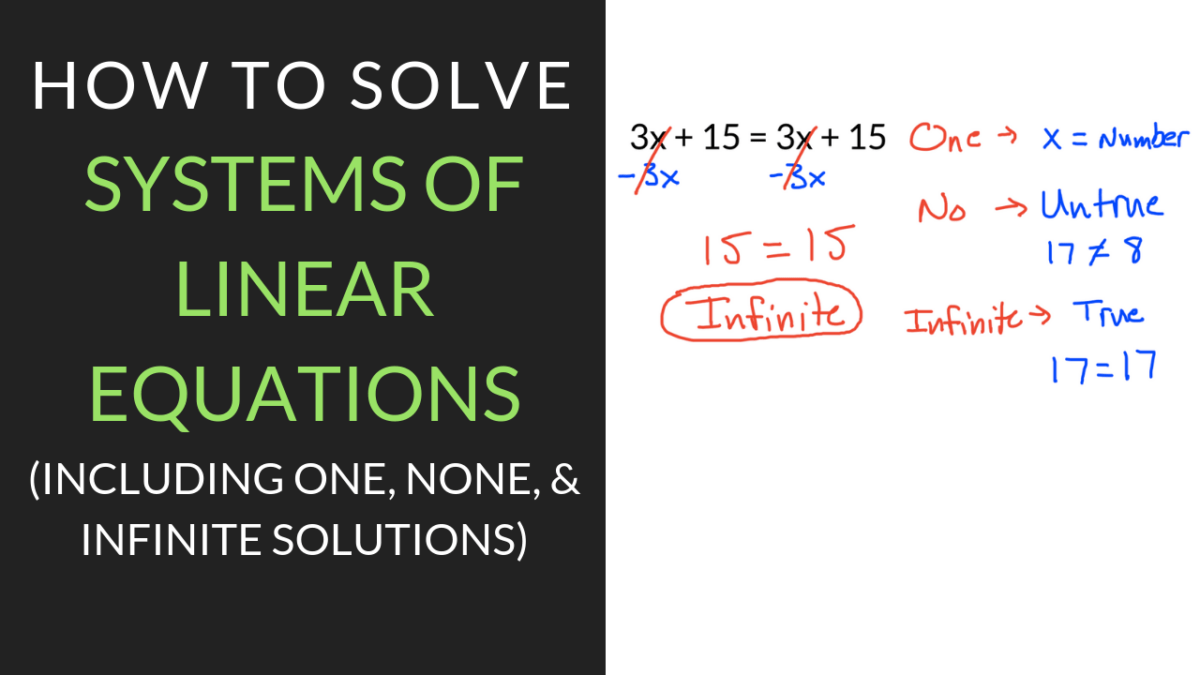
Then the order of operations is used to simplify the remaining solution. The numeric solution is substituted into the original problem. We must divide both sides by 3.Ī nice fact about solving linear equations is that the solutions can be checked. In order to finish up our example, let's perform the last step. Performing this step allows us to cancel the coefficient. If the variable is being divided by a number, then we multiply both sides of the equation by that number. If the variable is being multiplied by a number, then we divide both sides of the equation by that number. The next step involves cancelling the number next to the variable, and that number is called the coefficient. The subtraction by five can be undone by doing the opposite. To solve for "x," we have to do the reverse order of operations. The term that is either adding to or subtracting from the variable must be canceled first by doing the opposite, otherwise known as the inverse operation. With and, we now have a system of two equations in the variables ?b? and ?c?.Įliminate the parentheses, and combine like terms.Īctually, it isn’t impossible, but if something like that happens, it means that the original system of three equations has no solution.When solving linear equations of this form, we must carefully simplify the equation using a special two-step order. Now we’ll subtract equation from equation. This time we need to multiply equation by ?4?, so we can subtract it from equation and eliminate the variable ?a?. We need to get another equation in only the variables ?b? and ?c?. Now let’s subtract equation from equation, which will give us an equation in only the variables ?b? and ?c?.Įliminate the parentheses, and then combine like terms. Let’s multiply equation by ?3?, so we can eliminate the variable ?a? by subtracting the resulting equation from equation. So we’ll need to multiply one of the equations by some number such that by combining the resulting equation with one of the other two equations, we’ll be able to eliminate a variable.
None of the terms with the same variable have the same coefficient (or coefficients that are equal in absolute value but opposite in sign). Use any method to solve the system of equations. Now choose one of the three original equations, and plug in ?-1? for ?x? and ?-4? for ?z?, and then solve for ?y?. If we add these two equations, we can eliminate the variable ?z?, and then solve for ?x?.Ĭhoose one of the new equations, and plug in ?-1? for ?x?, and then solve for ?z?. The coefficients of ?z? in our two new equations are ?-2? and ?2?, respectively. You might have also noticed that the coefficients of ?y? in equations and are ?-5? and ?5?, respectively, so we can add these two equations to get another equation in only the variables ?x? and ?z?. Remove parentheses and combine like terms. If we add these two equations, the ?y? terms will cancel (we’ll eliminate the variable ?y?) and we’ll get an equation in only the variables ?x? and ?z?. Notice that the coefficients of ?y? in equations and are ?-5? and ?5?, respectively.


 0 kommentar(er)
0 kommentar(er)
